Optimization
🎯 Unconstrained Optimization
Exploring gradient-based optimization methods on classic test functions without constraints
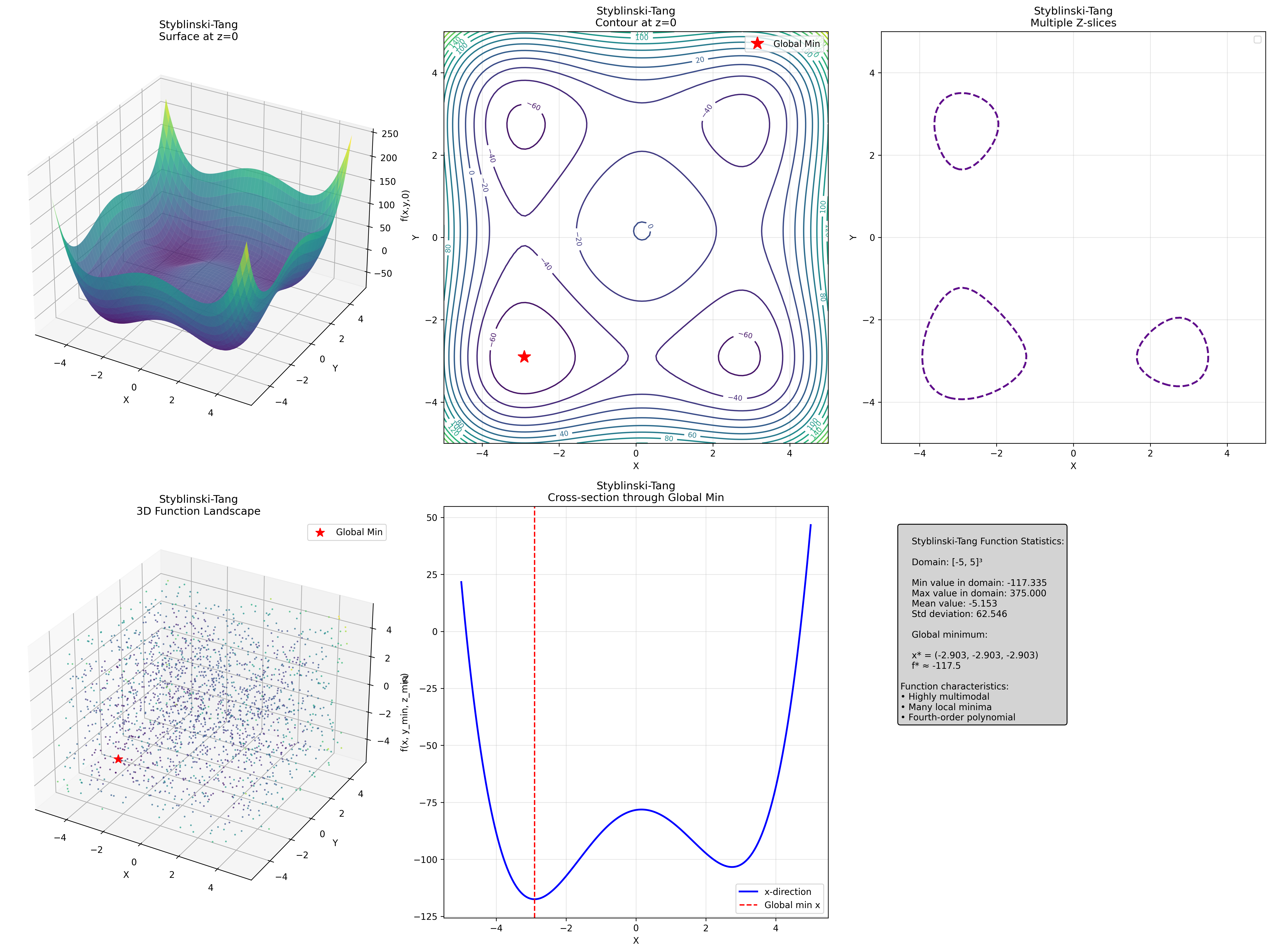
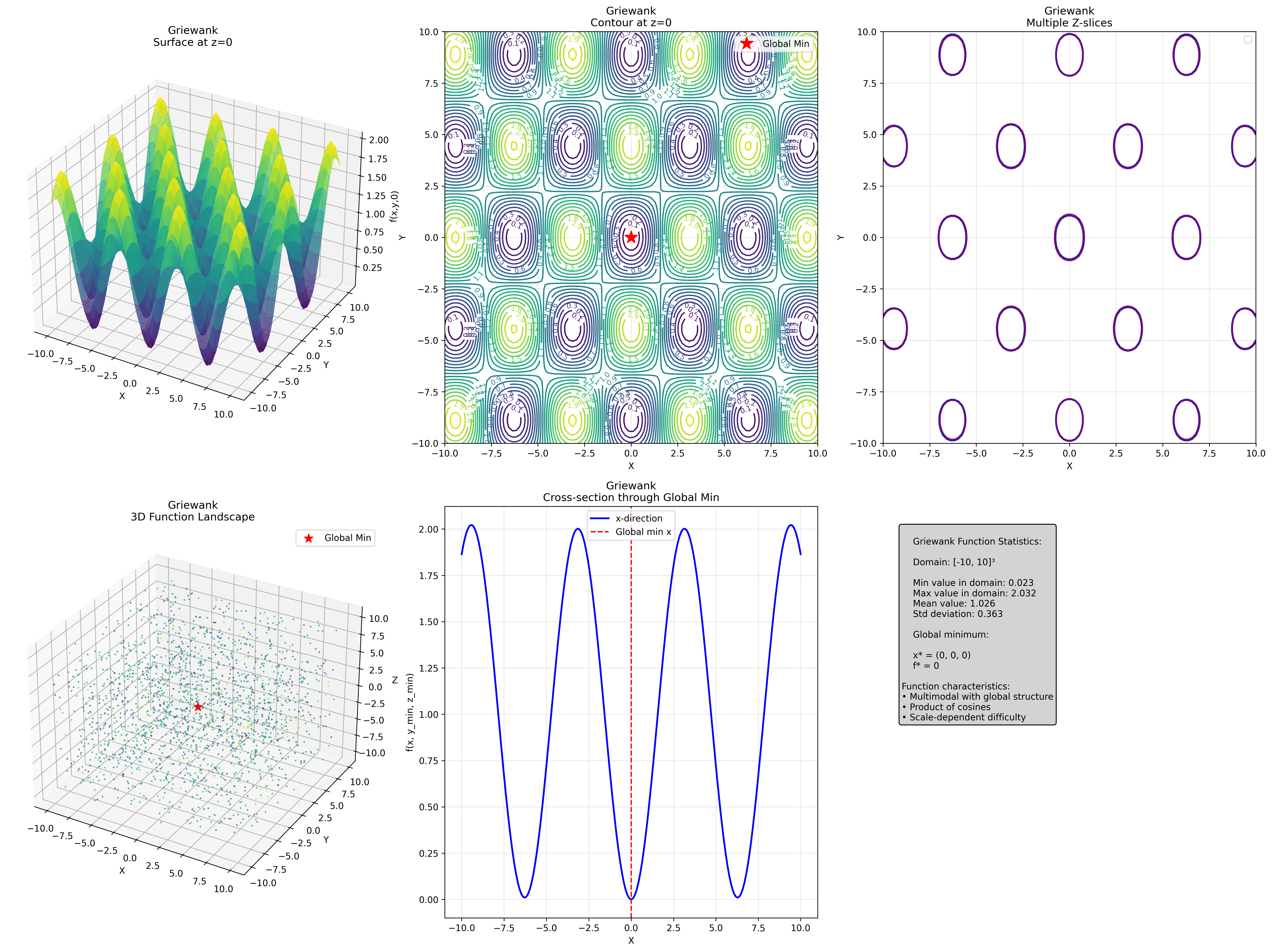
📐 2D Optimization Problems
Comparing Gradient Descent vs Conjugate Gradient methods on different landscape types:
⚖️ Constrained Optimization
Understanding how different solvers handle constraints in real-world optimization problems
🎯 The Solver Landscape
Optimization solvers can be categorized by their algorithmic approach and the order of derivative information they use. This landscape shows where popular solvers sit in this space:
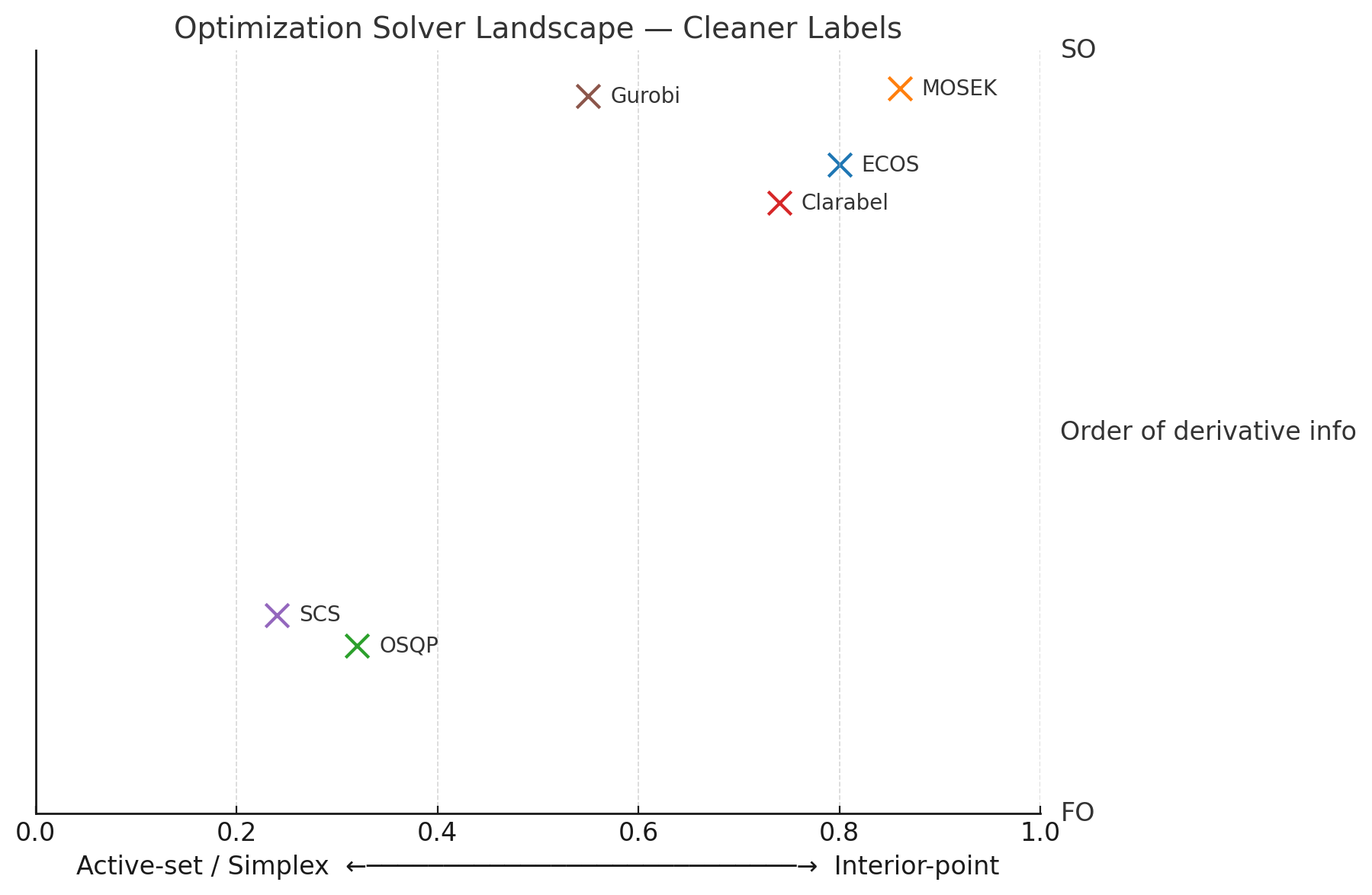
Key Insight: ECOS (Interior Point) and OSQP (Active Set) represent fundamentally different philosophies for handling constraints during optimization.
🔧 Constraint Philosophies
🚫 Interior Point (ECOS)
"Never Touch the Boundary"
- ✨ Maintains strict feasibility throughout
- 🛡️ Uses barrier functions to repel from constraints
- 📈 Smooth, monotonic convergence
- 🎯 Conservative but reliable approach
🤝 Active Set (OSQP)
"Walk Along the Boundary"
- 🎢 Identifies and moves along constraint boundaries
- ⚖️ May temporarily violate some constraints
- 🔄 Opportunistic exploration then correction
- 💡 Exploits constraint structure
💼 Real-World Application: Beta-Neutral Portfolio
We demonstrate the solver differences using a realistic quantitative finance problem: constructing a market-neutral portfolio that maximizes alpha while maintaining zero market exposure.
📈 Assets in the Portfolio:
⚡ Optimization Constraints
- Beta Neutrality: Portfolio beta = 0 (no market exposure)
- Full Investment: Sum of weights = 1 (100% capital deployed)
- Position Limits: -50% ≤ weight ≤ 50% (risk management)
- Objective: Maximize expected alpha minus risk penalty
🎬 Solver Animations
🔵 ECOS - Interior Point Method
Notice the smooth objective function improvement and consistent constraint satisfaction
🟠 OSQP - Active Set Method
Observe the "dip and rise" objective pattern as constraints are prioritized differently
⚖️ Side-by-Side Comparison
Direct comparison of constraint violation patterns and convergence behavior
🧠 Key Insights from the Animations
🎯 ECOS Behavior
Maintains strict feasibility throughout, smooth monotonic improvement, reaches stability earlier (~iteration 30)
🎢 OSQP Pattern
Shows "dip and rise" objective pattern, larger constraint violations during exploration, longer convergence time
📊 Constraint Handling
ECOS: simultaneous constraint satisfaction
OSQP: strategic constraint prioritization
🏆 Final Outcome
Both reach nearly identical optimal portfolios, but via fundamentally different paths
🎓 Educational Takeaways
🏛️ When to Use Interior Point (ECOS)
- 🔒 Regulated environments where constraint violations are unacceptable
- 📊 Convex problems with well-behaved constraints
- ⚡ Large-scale problems where global convergence properties matter
- 🛡️ Risk-averse applications requiring guaranteed feasibility
🔬 When to Use Active Set (OSQP)
- 🎯 Exploratory optimization to understand constraint trade-offs
- 📐 Problems with clear constraint structure (LP, QP)
- 🔄 Iterative design processes where constraint violations provide insight
- 💡 Applications requiring constraint sensitivity analysis
🔧 Technical Implementation
The animations were generated using:
- CVXPY: Convex optimization modeling framework
- ECOS: Embedded Conic Solver for interior point methods
- OSQP: Operator Splitting Quadratic Program solver
- Matplotlib: Animation framework for visualization
- NumPy: Numerical computing for portfolio calculations
Each solver's path was simulated to reflect their actual algorithmic behavior, with ECOS maintaining barrier margins and OSQP implementing active set identification strategies.